Discriminante e Relação entre os coeficientes e raízes da equação
Discriminante
1) O número ∆ =b^2-4ac é chamado discriminante da função quadrática $f(x)=ax^2+bx+c$.
2) Quando ∆> 0, a função $f(x)=ax^2+bx+c$ tem raízes reais distintas.
Quando ∆= 0, a função $f(x)=ax^2+bx+c$ tem raízes reais e iguais.
Quando ∆< 0, a função $f(x)=ax^2+bx+c$ não existirá raízes reais.
3) Relação entre os coeficientes e raízes da equação $ax^2+bx+c$, com a≠0
Existindo zeros reais tal que:
$x'=\frac{-b+√∆}{2a}$ e $x''=\frac{-b-√∆}{2a}$, onde obtemos
$x'+x''=\frac{-b+√∆}{2a}+\frac{-b-√∆}{2a}$=
$x'+x''=\frac{-2b+√∆-√∆}{2a}$=
$x'+x''=\frac{-2b}{2a}=-\frac{b}{a}$
Observe que $\frac{(x'+x'')}{2}=-\frac{b}{2a}$, ou seja, a média aritmética das raízes é
$-\frac{b}{2a}$, o que significa que as raízes são equidistantes do ponto $-\frac{b}{2a}$. Disso decorre que $f(x_1)=f(x_2)$, para $x_1\neq\,x_2$ se, e se somente se, os pontos $x_1$ e $x_2$ são equidistantes de $-\frac{b}{2a}$.
$x' . x''=\frac{-b+√∆}{2a}.\frac{-b-√∆}{2a}$=
$x' . x''=\frac{b^2-(√∆)^2}{4a^2}=\frac{\bcancel{b^2}-\bcancel{b^2}+4ac}{4a^2}=\frac{c}{a}$
logo $x' . x''=\frac{c}{a}$
4) Forma fatorada do Trinômio $ax^2+bx+c$, com a $\neq$ 0
Quando $\delta$ $\ge$ 0. ou seja , quando a equação $ax^2+bx+c=0$ possui as raízes reais x' e x''.
Podemos escrever:
$ax^2+bx+c=a\large(x^2+\frac{b}{a}+\frac{c}{a})$=
$=a[x^2 -(x'+x'')x+x'x'']$=
$=a[x^2 -xx'+x''x+x'x'']$=
$=a[ x(x-x') -x''(x-x')]$=
$=a(x-x')(x-x'')$=
Logo a forma fatorada da função do 2º grau é:
$ax^2+bx+c=a(x-x')(x-x'')$,
Texto tirado do Livro Dante Matemática volume único pág 76 à 77.
Caso haja algum erro comente aqui ou nos envie um email: fmbacelar@gmail.com


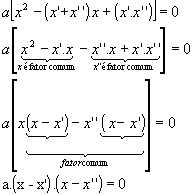


Post A Comment:
0 comments:
Segue alguns símbolos, caso necessitem utilizá-los:
____________________________________________
α β γ δ ∆ λ μ Ω ο ρ φ χ ψ ξ ε η θ π ∂ ∑ ∏ ℮ אօ ∞ ℝ ℕ ℚ ℤ Ø f◦g
½ ¼ ¾ ½ ⅓ ⅔ ⅛ ⅜ ⅝ ⅞ ² ³ ¹ º ª ₁ ₂ ₃ ₄ ≈ ≠ ≡ ∀ ∃ ⇒ ⇔ → ↔
∈∋∧ ∨ ⊂ ⊃ ∩ ∪ − + × ± ∓ ÷ √ ∛ ∜ ⊿∟ ∠→ ↑ ↓ ↕ ← ≤ ≥
outros
√ ∇ ∂ ∑ ∏ ∫ ≠ ≤ ≥ ∼ ≈ ≅ ≡ ∝ ⇒ ⇔ ∈ ∉ ⊂ ⊃ ⊆ ⊇ \ ∩ ∪ ∧ ∨ ∀ ∃ ℜ ℑ