Máximos e Mínimos (Cálculo)

1. Introdução

No contexto do estudo de derivadas, resolvemos problemas de funções quadráticas onde se pretendia encontrar o valor ótimo que estas assumiam, ou seja, o seu valor máximo.

O ponto máximo, onde o coeficiente angular é zero, geralmente era único, o que nos permitia igualar a derivada da função a zero e, em seguida, resolve-las em x.

Um exemplo é a função lucro, representada por a qual você deve esboçar o gráfico e constatar as informações acima.

Entretanto nem sempre é tão simples assim, pois, de maneira geral, nem todo ponto da função no qual a derivada é nula é o pico do gráfico.

Temos duas funções cujas derivadas em x = 0  são nulas. Ambas possuem tangentes horizontais em (0;0), mas a função y = x²  alcança seu valor mínimo em (0;0), enquanto que a função y = x³ não possui máximo nem mínimo  neste ponto.
A situação torna-se mais complicada com a existência de funções que possuem máximos e mínimos em pontos nos quais as derivadas nem sequer são definidas, como ilustramos nas figuras 3 e 4.



Vemos então uma forma sistematizada de locação e identificação de máximos e mínimos de funções diferenciáveis. Neste processo você também aprenderá como usar derivadas que o ajudarão a construir gráficos de funções.



2. Máximos e Mínimos Relativos

Um máximo relativo de uma função é um “pico”, o ponto máximo do gráfico em relação a qualquer outro ponto vizinho a ele no gráfico.
Um mínimo relativo é um “fundo de vale”, o ponto mínimo do gráfico em relação a qualquer outro ponto vizinho. A função representada na figura 5 possui um máximo relativo em x = b, e mínimos relativos em       x = a  e  x = c. Note que o máximo relativo não precisa ser o ponto mais alto do gráfico, é máximo somente em relação aos pontos vizinhos. Da mesma forma, o mínimo relativo não é o ponto “mais baixo” do gráfico.

   



Conhecendo-se os intervalos nos quais a função é crescente ou decrescente, pode-se facilmente identificar os máximos e mínimos relativos da função. O máximo relativo ocorre quando a função deixa de ser crescente e passa a ser decrescente. O mínimo relativo ocorre quando a função deixa de ser decrescente e passa a ser crescente.


3. Sinal da Derivada

Pode-se reconhecer quando uma função é crescente ou decrescente através do sinal da sua derivada, porque a derivada é o coeficiente angular da reta tangente. Quando a derivada é positiva, o coeficiente angular da tangente é positivo e a função é crescente. Caso contrário, quando a derivada é negativa, o coeficiente angular é negativo e a função é decrescente. A figura 6 ilustra essa situação.

Conclusão:

Se f (x) > 0, quando a < x < b, então f é crescente para a < x < b
Se f (x) < 0, quando a < x < b, então f é decrescente para a < x < b



4. Pontos Críticos

Sendo $x_0$   um ponto pertencente ao domínio de uma função f (x), diz-se que  $x_0$  é abscissa de um ponto crítico se:

A função é crescente quando sua derivada é positiva e decrescente quando sua derivada é negativa, os únicos pontos nos quais a função pode assumir máximos ou mínimos relativos são aquelas nos quais as derivadas são nulas ou indefinidas.

O ponto crítico da função é aquele no qual a derivada é nula ou indefinida. Todo extremo relativo é um ponto crítico, mas nem todo ponto crítico é um extremo relativo.

1) f ($x_0$) = 0
2) f ($x_0$)) não está definida

Observe que:

1) Se o sinal da derivada for positivo à esquerda do ponto crítico e negativo à direita dela, o ponto é um máximo relativo. (fig. 7a).

2) Se o sinal da derivada for negativo à esquerda do ponto crítico e positivo à direita dela, o ponto é um máximo relativo. (fig. 7b).

3) Se o sinal da derivada for o mesmo em ambos os lados do ponto crítico, o ponto não é máximo nem mínimo relativo. (fig. 7c).




5. Teorema de FERMAT (Condições necessárias para a existência de extremo relativo):
Seja  f  definida em  (a;b)  e $x_0$ $\in$ (a;b). Se  f   assume um extremo relativo em  x  e  f (x)  existe,  então  f ($x_0$) = 0.

6. Seja  f  uma função contínua em [a;b] e derivável em ]a;b[ :

a) f é crescente em [a;b]$\Leftrightarrow$ f(x)$\geq$0
b) f é decrescente em [a;b]$\Leftrightarrow$ f(x)$\leq$0



Teste da Derivada Primeira para Extremos Relativos:

Seja  f  contínua em [a;b] e  $x_0$ $\in$ ]a;b[ Suponhamos que f  seja derivável em ]a;b[ exceto possivelmente em $x_0$ .

a) se f (x) > 0 para x < $x_0$ e f (x) < 0 para x > $x_0$ então  é o ponto máximo relativo.
b) se f (x) < 0 para x < $x_0$ e f (x) > 0 para x > $x_0$ então  é o ponto mínimo relativo.



Teste da Derivada Segunda para Extremos Relativos:

Seja  f  derivável em ]a;b[. Se  é tal que f (x) existe e é contínua em V(x) então:

a) se f ” $x_0$ < 0, $x_0$ é o ponto máximo relativo.
b) se f ”$x_0$ > 0, $x_0$ é o ponto mínimo relativo.

Máximos e Mínimos Absolutos:

Na Maioria dos problemas práticos de otimização, o objetivo é calcular o máximo absoluto ou mínimo absoluto de uma certa função num intervalo e não o máximo ou mínimo relativo. O máximo absoluto de uma função  no intervalo é o maior valor da função neste intervalo. O mínimo absoluto é o menor valor.
Frequentemente, os extremos absolutos coincidem com os relativos. No intervalo a$\leq$x$\leq$b, o máximo absoluto e o máximo relativo coincidem, porém o mínimo absoluto ocorre na extremidade de x = a, que não é um mínimo relativo.

Extremos Absolutos em Intervalos Fechados:

Uma função contínua num intervalo fechado alcança um máximo absoluto e um mínimo absoluto no intervalo.

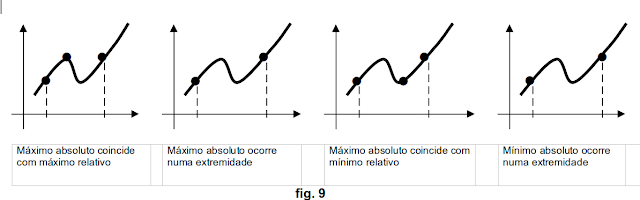
O extremo absoluto pode coincidir com o extremo relativo ou ocorrer no extremo x = a ou x = b. A figura 9 ilustra estas possibilidades.

Usando estas observações, podemos descrever uma técnica simples de localização e identificação dos extremos absolutos de funções contínuas em intervalos fechados.

Como Calcular Extremos Absolutos de uma Função Contínua f num Intervalo Fechado [a;b].

1^o Passo: Calcule as coordenadas x de todos os pontos críticos de f no intervalo .

2^o Passo: Calcule f (x) nestes pontos críticos e nas extremidades x = a e x = b.

3^o Passo: Selecione os maiores e menores valores de f (x) conseguidos no 2^o Passo. Você obterá, então,

respectivamente, o máximo absoluto e mínimo absoluto.

Extremos Absolutos em Intervalos não Fechados

Quando o intervalo no qual desejamos maximizar ou minimizar a função não é da forma [a;b], precisamos modificar a técnica, porque, não é garantida a existência de extremos absolutos da função no intervalo em questão. Por outro lado, se um extremo absoluto existe e a função é contínua, o extremo absoluto coincidirá com o extremo relativo ou com uma extremidade contida no intervalo. A figura 10 ilustra algumas dessas possibilidades.

Para calcular os extremos absolutos de uma função contínua num intervalo que não seja fechado, calculamos o valor da função nos pontos críticos e nas extremidades contidas no intervalo, pois a função possui extremos relativos neste intervalo.

7. Teorema do Valor Extremo

Se f é contínua em [a;b], então possui um valor máximo absoluto e um valor mínimo absoluto.

Concavidade

Diz-se que uma curva tem concavidade para baixo quando sua tangente se move no sentido dos ponteiros do relógio, ao percorre a curva da esquerda para a direita.

Diz-se que uma curva tem concavidade para cima quando sua tangente se move no sentido contrário ao dos ponteiros do relógio, ao percorre a curva da esquerda para a direita.

Concavidade e Coeficiente Angular da Tangente

Quando a curva tem concavidade para cima (como na fig. 6-a), o coeficiente angular de sua tangente cresce quando x aumenta de valor. Quando a curva tem concavidade para baixo (como na fig. 6-b), o coeficiente angular da sua tangente decresce quando x aumenta de valor.

Sinal da Derivada Segunda

A relação entre concavidade e coeficiente angular da tangente determina uma caracterização simples de concavidade em termos de sinal da derivada Segunda. Suponha que a derivada Segunda f “ seja positiva num intervalo. Logo, a derivada Primeira f ‘ é crescente no intervalo. Mas f ‘ é o coeficiente angular da tangente, portanto, é crescente e a curva do gráfico de f tem concavidade para cima no intervalo. Por outro lado, se f “ é negativo no intervalo, então f ‘ é decrescente e a curva do gráfico de f tem concavidade para baixo no intervalo.

Significado geométrico do sinal da derivada Segunda:

a) se f “ (x) > 0 quando a < x < b, então, f tem concavidade para cima em a < x < b.

b) se f “ (x) < 0 quando a < x < b, então, f tem concavidade para baixo em a < x < b.

Pontos de Inflexão

O ponto no qual ocorre a variação de concavidade da função denomina-se ponto de inflexão. Se a derivada Segunda é definida no ponto de inflexão, seu valor tem que ser zero. Os pontos de inflexão podem ocorrer onde a derivada Segunda é indefinida.

Os pontos nos quais a derivada Segunda da função é nula ou indefinida denominam-se pontos críticos de Segunda ordem.

Construção de Gráficos

Devemos seguir os seguintes passos, para obter o gráfico da função f (x):

1. Explicite o domínio;
2. Calcule a derivada Primeira e, em seguida, as coordenadas x dos pontos críticos de primeira ordem, igualando f ‘ (x) a zero e resolvendo a equação em x. Não esqueça de incluir também valores de x para os quais a derivada é indefinida. Substitua estes valores de x na função f (x), obtendo as coordenadas y dos pontos críticos.
3. Calcule a derivada Segunda f “ (x). Proceda como no passo anterior.
4. Estude o sinal da Primeira derivada e determine onde f (x) é crescente ou decrescente. Destaque os pontos Máximo e Mínimo.
5. Estude a concavidade de f (x), verificando o sinal da Segunda derivada. Destaque os pontos de inflexão.
6. Determine as equações das assíntotas verticais e obliquas e as interseções com os eixos coordenados...
7. Construa o gráfico.

 

Exercícios

1. Para as funções abaixo, pede-se:

1. Domínio e imagem;
2. Seus intervalos de crescimento ou decrescimento;
3. Seus extremos relativos;
4. Seus pontos de inflexão;
5. Assíntotas
6. Esboçar seus gráficos.

a)

b)

c)

d)

e)

f)

 

2. Uma empresa possui a Receita e o Custo dados pelas equações Para o intervalo de produção de 0 a 6 unidades, determine:

1. A produção para que o Custo seja mínimo;
2. Os intervalos em que a função Custo cresce ou decresce;
3. A produção para que a Receita seja máxima;
4. Os intervalos em que a Receita cresce ou decresce;
5. A produção para que o Lucro seja máximo;
6. O Ponto de Ruptura.

3. Suponha que a equação de demanda para uma certa mercadoria seja p = 4 – 0,0002x, onde x é o número de unidades produzidas semanalmente e p reais é o preço de cada unidade. O número do custo total da produção de x unidades é 800 + 3x. Se o lucro semanal deve ser o maior possível, encontre o número de unidades que serão produzidas semanalmente, o preço de cada unidade e o lucro semanal.

R: x = 2500 p = R$ 3,50 L = R$ 450,00

4. Verificar os intervalos de crescimento e decrescimento da função

R: x > -10 f é crescente x < -10 f é decrescente

5. Determine os intervalos em que a função é crescente, decrescente, determine os extremos relativos e esboce seu gráfico.

R: x < -2; x > 1 f é crescente -2 < x < 1 f é decrescente .

x = -2 é abscissa de pto de máx (-2; 13) x = -2 é abscissa de pto de mín (1; -14)

 Até mais!

Ajude-nos a continuar este trabalho!
Os Doadores tem direito a Resoluções de Questões Grátis dependendo de sua doação.