O número de Euler
A base do logarítmo natural é o número de Euler, simbolizado por: e, ele é obtido pela definição do logaritmo natural, esse número corresponde á área sob a curva da função:  , quando seu valor é unitário, ou seja:
, quando seu valor é unitário, ou seja:
mais formalmente:
O valor deste número pode ser encontrado por aproximação, utilizando-se os métodos de análise de seqûencias e séries, encontrados no livro: Cálculo (Volume 3).
A equação que fornece o valor do número de Euler é dada a seguir:
Nesta equação podemos observar que quanto mais alto o valor de n mais preciso se torna o valor de e.
De maneira simplificada, com base nos conceitos até agora abordados podemos encontrá-la da seguinte maneira:
Se  então
então  , logo:
, logo: 
Por outro lado, pela definição:
Para  :
:
Sendo:  e
e 
Concluimos que:
Teoremas
A maioria dos teoremas relacionados, têm origem nas conclusões obtidas no estudo do logarítmo natural, dos quais relacionamos os mais usados:
T39 - Soma
Seja a função  , pode-se afirmar que:
, pode-se afirmar que:
Comprovação:
Considerando:  e
e  ,
,
logo:
sendo:  e
e  ,
,
O que comprova o teorema.
T40 - Subtração
De forma similar à análise anterior, sendo a função  , pode-se afirmar que:
, pode-se afirmar que:
Comprovação:
Considerando:  e
e  ,
,
logo:
sendo:  e
e  ,
,
O que comprova o teorema.
T41 - Potência
Seja a função  , pode-se afirmar que:
, pode-se afirmar que:
Comprovação:
O que comprova o teorema.
Derivadas
Consideremos que  , e conseqüentemente:
, e conseqüentemente:  , se derivarmos implicitamente este expressão:
, se derivarmos implicitamente este expressão:
Curiosamente, teremos:
Ou seja, a função exponencial natural é invariável durante o processo de derivação, o que traz uma série de implicações simplificadoras para estas funções.
Por outro lado se  , temos que:
, temos que:
Fazendo  e
e 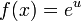 , teremos:
, teremos:
Se  , concluimos que:
, concluimos que:
Que é adotada como uma derivada mais genérica, pois pode ser empregada em qualquer exponencial, pois inclui correção para o fator da base.
Integrais
Como não poderia ser diferente, o valor da integral da função exponencial natural  é a própria função, conforme a regra da reversibilidade entre a derivada e a integral, apenas sendo necessária a devida observação da base, para eventual correção da diferencial e conseqüente introdução de fator de correção, nos casos em que a função torna-se composta.
é a própria função, conforme a regra da reversibilidade entre a derivada e a integral, apenas sendo necessária a devida observação da base, para eventual correção da diferencial e conseqüente introdução de fator de correção, nos casos em que a função torna-se composta.
Desta forma, temos:
,
Sendo C constante.
Logarítmicas com outras bases
Como foi visto durante o ensino médio, os logaritmos têm uma definição direta e que denota a sua finalidade de expressar o valor do expoente em uma operação exponencial, a definição pura é dada da seguinte forma:
Se  então,
então,
Onde: a é chamada base do logaritmo, x é o logaritmando e n é o expoente.
O logaritmo é, portanto, a operação pela qual se obtém o expoente necessário para que a base seja elevada, numa operação exponencial e se obtenha o número x.
A função logarítmica de base a pode ser expressa da seguinte forma:
O que nos possibilita encontrar um valor para cada x expresso na equação.
Mudança de base
Analisemos agora a possibilidade de encontrar uma função logarítmica de uma base a e transformá-la em uma função logarítmica de base natural, ou outra base qualquer:
Seja a função  , podemos dizer que:
, podemos dizer que:
como:  ,
,
O que nos possibilita afirmar que:
,
ou
.
Note que a analogia serve para funções logarítmicas de qualquer base, visto que podemos substituir  por
por  sendo z a base que substituirá e na análise anterior.
sendo z a base que substituirá e na análise anterior.
O que nos possibilita considerar que quando temos duas bases, sejam: a e b, podemos promover a troca das bases, de forma que:
Derivadas
A derivada da função logarítmica com base diferente de e pode ser feita por substituição da base. Considerando  , temos que:
, temos que:
logo:
Que nos dá a derivada:
Fonte:http://pt.wikibooks.org/





Post A Comment:
0 comments:
Segue alguns símbolos, caso necessitem utilizá-los:
____________________________________________
α β γ δ ∆ λ μ Ω ο ρ φ χ ψ ξ ε η θ π ∂ ∑ ∏ ℮ אօ ∞ ℝ ℕ ℚ ℤ Ø f◦g
½ ¼ ¾ ½ ⅓ ⅔ ⅛ ⅜ ⅝ ⅞ ² ³ ¹ º ª ₁ ₂ ₃ ₄ ≈ ≠ ≡ ∀ ∃ ⇒ ⇔ → ↔
∈∋∧ ∨ ⊂ ⊃ ∩ ∪ − + × ± ∓ ÷ √ ∛ ∜ ⊿∟ ∠→ ↑ ↓ ↕ ← ≤ ≥
outros
√ ∇ ∂ ∑ ∏ ∫ ≠ ≤ ≥ ∼ ≈ ≅ ≡ ∝ ⇒ ⇔ ∈ ∉ ⊂ ⊃ ⊆ ⊇ \ ∩ ∪ ∧ ∨ ∀ ∃ ℜ ℑ