"A Equação da Hipérbole" - O Baricentro da Mente

A Equação da Hipérbole

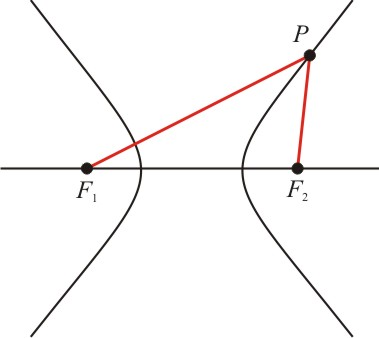
Definição: A hipérbole é o lugar geométrico dos pontos de um plano cuja diferença das distâncias, em valores absolutos, a dois pontos fixos desse plano é constante.

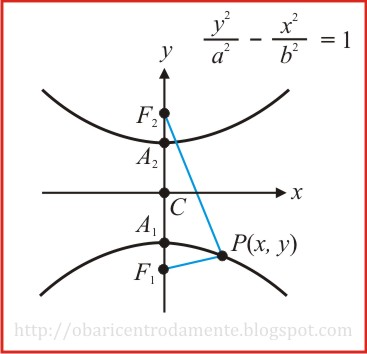
Sejam dois pontos distintos F₁ e F₂ de um plano π, cuja distância d(F₁ , F₂) = 2c. Seja um número real a tal que 0 < 2a < 2c.

Hipérbole é o conjunto de todos os pontos P do plano, tais que:

ou

[Figura 1: Hipérbole]

Como podemos ver, a hipérbole é uma curva com dois ramos. Analisando a equação (2), podemos ver que um ponto P está na hipérbole se, e somente se:

Quando P está no ramo da direita, a diferença é igual a +2a:

e quando P estiver no ramo da esquerda, a diferença será – 2a:

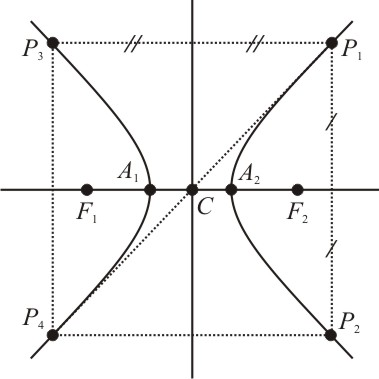
Considerando a reta que passa por F₁ e F₂, as intersecções com a hipérbole serão os pontos A₁ e A₂. Traçamos uma perpendicular a esta reta, passando pelo centro C do segmento F₁ e F₂.

[Figura 2: Eixos de Simetria da Hipérbole]

A hipérbole é uma curva simétrica em relação às estas duas retas, como também ao ponto C. Se P₁ é um ponto da hipérbole, existem outros pontosP₂, P₃ e P₄ tais que: P₂ é o simétrico de P₁ em relação à reta horizontal; P₃ é o simétrico de P₁ em relação à reta vertical; P₄ é o simétrico a P₁ em relação ao ponto C. Pela simetria, concluímos que:

Elementos da Hipérbole

Os principais elementos de uma hipérbole estão relacionados abaixo, considerando a figura 3:

[Figura 3: Elementos da Hipérbole]

Focos: F₁ e F₂

Distância focal: é a distância 2c entre os focos, onde c = CF₁=CF₂

Centro: é o ponto médio C do segmento F₁F₂

Eixo real ou transverso: é o segmento A₁A₂, de comprimento 2a, onde a =CA₁ = CA₂

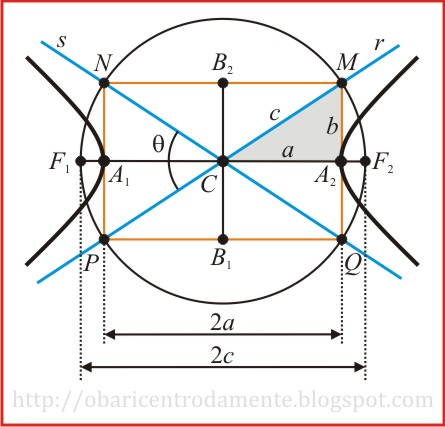
Eixo imaginário ou conjugado: é o segmento B₁B₂, de comprimento 2b. O valor de b é definido pela relação pitagórica:

onde a, b e c são as medidas dos lados do triângulo retângulo CA₂M.

Assíntotas: são as retas r e s das quais a hipérbole se aproxima cada vez mais à medida que os pontos se afastam dos focos. Esta aproximação é contínua e lenta de forma que a tendência da hipérbole é tangenciar suas assíntotas no infinito.

Considerando uma circunferência de raio CF₁ ou CF₂, cujo centro C é o mesmo centro da hipérbole, traçamos pelos vértices A₁ e A₂ cordas perpendiculares ao segmento F₁F₂ e marcamos as intersecções com a circunferência. Esses pontos são os vértices do retângulo MNPQ inscrito à circunferência. Esse retângulo tem dimensões 2a e 2b.

As retas r e s que contém as diagonais desse retângulo são as assíntotas da hipérbole.

Abertura: o ângulo θ é chamado de abertura da hipérbole

Excentricidade: a excentricidade e da hipérbole é o número dado pela relação:

A excentricidade da hipérbole está intimamente relacionada com sua abertura. Se mantivermos o segmento c fixo e variarmos apenas o comprimento do segmento a, teremos uma abertura maior quando a é menor e vice-versa. Então, se diminuirmos o valor de a teremos uma excentricidade maior e = c /a. Assim os ramos da hipérbole estarão mais abertos.

Quando a = b o retângulo MNPQ se transforma num quadrado, torando as assíntotas perpendiculares e a abertura da hipérbole será igual a θ = 45°. Para este caso específico a hipérbole recebe o nome de Hipérbole Equilátera.

Equação Reduzida da Hipérbole

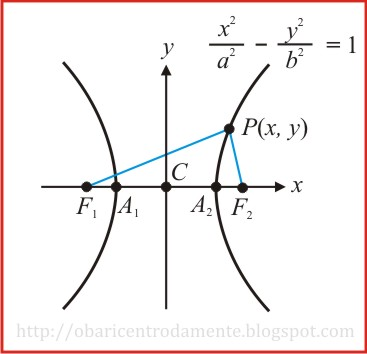
1º Caso: O Eixo Real está sobre o Eixo dos x:

Tomando um sistema ortogonal, com o centro C da hipérbole na origem do sistema, temos que:

[Figura 4: Eixo rel sobre eixo dos x]

Seja um ponto P(x, y) da hipérbole, cujos focos são os pontos F₁(– c,0) e F₂(c,0). Por definição temos que:

Em coordenadas:

Quadramos ambos os lados:

Quadramos novamente ambos os lados:

Substituímos a relação (4) na (5), obtendo:

Dividindo ambos os lados por a²b², resulta em:

Que é a equação da hipérbole.

2º Caso: O Eixo Real está sobre o Eixo dos y:

Tomando um sistema ortogonal, com o centro C da hipérbole na origem do sistema, temos que:

[Figura 5: Eixo real sobre o eixo dos y]

Analogamente ao primeiro caso, chegamos à equação da hipérbole:

Referências

[1] Geometria Analítica – Steinbruch & Winterle

[2] Matemática: Ciência e Aplicações V3 – Iezzi, Dolce, Et al

---

Veja mais:A Equação da Elipse
Um modo de Calcular a Integral Indefinida da Hipérbole no blog Fatos Matemáticos
Os Modelos Hiperbólicos de Crochê no blog Matheusmathica