Função de 1º GRAU - Questões para ENEM -MED

(Acafe) O soro antirrábico é indicado para a profilaxia da raiva humana após exposição ao vírus rábico. Ele é apresentado sob a forma líquida, em frasco ampola de 5mL equivalente a 1000UI (unidades internacionais). O gráfico abaixo indica a quantidade de soro (em mL) que um indivíduo deve tomar em função de sua massa (em kg) em um tratamento de imunização antirrábica.

l A lei da função representada no gráfico é dada por q = 0,2 . m, onde q é a quantidade de soro e m é a massa.

ll O gráfico indica que as grandezas relacionadas são inversamente proporcionais, cuja constante de proporcionalidade é igual a 1/5.

lll A dose do soro antirrábico é 40UI/Kg.

lV Sendo 3000UI de soro a dose máxima recomendada, então, um indivíduo de 80 Kg só po derá receber a dose máxima.

V Se um indivíduo necessita de 2880UI de soro, então, a massa desse indivíduo é de 72,2 Kg.

Todas as afirmações corretas estão em:

 a)I - III - IV

 b)I - III - IV - V

 c)II - III - IV - V

 d)I - II - V

Comente e peça a resolução!

(Enem) No Brasil há várias operadoras e planos de telefonia celular.
Uma pessoa recebeu 5 propostas (A, B, C, D e E) de planos telefônicos. O valor mensal de cada plano está em função do tempo mensal das chamadas, conforme o gráfico.

 
Essa pessoa pretende gastar exatamente R$ 30,00 por mês com telefone.
Dos planos telefônicos apresentados, qual é o mais vantajoso, em tempo de chamada, para o gasto previsto para essa pessoa?
a)A.
b)B.
c)C.
d)D.
e)E.
Peça a resolução da questão nos comentários

(Enem) Tanto na natureza, quanto na indústria, existem diversos tipos de fluidos. Fluidos Newtonianos são aqueles que apresentam crescimento linear da tensão cisalhante com relação ao gradiente de velocidade, com coeficiente angular não nulo. Apresentam ainda tensão cisalhante nula com gradiente de velocidade zero. A figura apresenta a relação da tensão cisalhante com o gradiente de velocidade para diversos tipos de fluidos.
 

Dentre as curvas da figura, determine qual(is) é(são) de fluido(s) Newtoniano(s).
a)A.
b)B.
c)C.
d)D.
e)A e C.

(ENEM) O cristalino, que é uma lente do olho humano, tem a função de fazer ajuste fino na focalização, ao que se chama acomodação. À perda da capacidade de acomodação com a idade chamamos presbiopia. A acomodação pode ser determinada por meio da convergência do cristalino. Sabe-se que a convergência de uma lente, para pequena distância focal em metros, tem como unidade de medida a diopria (di).

A presbiopia, representada por meio da relação entre a convergência máxima Cmax (em di) e a idade T (em anos), é mostrada na figura seguinte.
Considerando esse gráfico, as grandezas convergência máxima Cmax e idade T estão relacionadas algebricamente pela expressão
A) $C_{max} = 2^{-T}$
B) $C_{max}= T^ 2- 70T + 600$
C) $C_{max}= log_{2} (T^2 - 70T + 600)$
D) $C_{max} = 0,16T + 9,6$
E)$C_{max} = – 0,16T + 9,6$

(Enem)Um dos grandes desafios do Brasil é o gerenciamento dos seus recursos naturais, sobretudo os recursos hídricos. Existe uma demanda crescente por água e o risco de racionamento não pode ser descartado. O nível de água de um reservatório foi monitorado por um período, sendo o resultado mostrado no gráfico. Suponha que essa tendência linear observada no monitoramento se prolongue pelos próximos meses.

Nas condições dadas, qual o tempo mínimo, após o sexto mês, para que o reservatório atinja o nível zero de sua capacidade?

a) 2 meses e meio.

b) 3 meses e meio.

c) 1 mês e meio.

d) 4 meses.

e) 1 mês.

(Enem) Uma torneira gotejando diariamente é responsável por grandes desperdícios de água. Observe o gráfico que indica o desperdício de uma torneira:

Podemos dizer que em 35 dias o desperdício foi de
A) 600 litros.
B) 900 litros.
C) 1200 litros.
D) 1800 litros.
E) 2100 litros.

SABEMOS QUE É UMA FUNÇÃO ESCALAR TIPO f(x)=ax, pois o b=0 

como a função é

Volume x tempo

Assim fica V(t)=at

com nos pontos incidentes (5,300) e (10, 600)

o coeficinete angular é

$a=\frac{y-y_0}{x-x_0}=\frac{600-300}{10-5}=\frac{300}{5}=60$

f(x)=60x

f(35)=60x35=2100litros

letra E

 (Espm 2017) O gráfico abaixo mostra a variação da temperatura no interior de uma câmara frigorífica desde o instante em que foi ligada. Considere que essa variação seja linear nas primeiras 2 horas.

O tempo necessário para que a temperatura atinja -18°C é de:

a)90 min

b)84 min

c)78 min

d)88 min

e)92 min

Resposta:[B]

O gráfico é uma função linear decrestente ou seja o coeficiente angular é negativo

assim temos a função temperatura(T) x tempo(t)

T(t)=ax+b

  (48, 0)

 assim o coeficiente angular

b=24

x=48

T(t)=0

substiuindoc

T(48)=ax+b 

0=a.48+24

$a=\frac{\cancel{-24}^{:24}}{\cancel{48}^{:24}}=-\frac{1}{2}$

 

Queremos calcular o valor de t para o qual se tem T(t) = - 18ºC. Desse modo,

vem : 
$–18 =-\frac{1}{2}t+24$
$\frac{1}{2}t=18+24$
$\frac{1}{2}t=42$
$\boxed{t=84min}$

(Unifenas MG) A cada incursão respiratória, um paciente em ventilação mecânica, deve receber um volume de ar de acordo com sua massa corporal conforme o seguinte gráfico:

Um paciente de massa corporal 62 kg recebe um volume de ar, em mL, correspondente a 

a) 343.

b)372.

c)350.

d)434.

e)420.

 Calcularemos primeiramente o coeficiente angular

$a=\frac{\Delta y}{\Delta x}=\frac{294,0-227,5}{42,0-32,5}$
$=\frac{66,5}{9,5}=\frac{665^{:5}}{95^{:5}}=\frac{133}{19}=7$

SABEMOS QUE É UMA FUNÇÃO ESCALAR TIPO f(x)=ax, pois o b=0 

como a função é

Volume de ar (ml) x massa corporal(kg)

Assim fica V(m)=am

dados 

m=62kg

a=7 

V(m)=7.m 

V(65)=7 . 65

V(65)=434

 

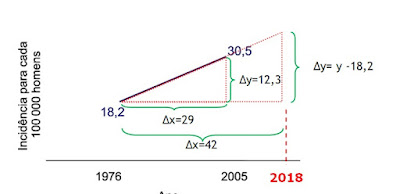
 (SANTA CASA SP) O gráfico ilustra o aumento da incidência da doença de Parkinson entre homens no período de 1976 a 2005.

Considerando esse aumento linear, e que ele se mantenha até os dias atuais, espera-se que a incidência dessa doença em 2018, para cada 100 000 homens, seja próxima de

a) 31,8.

b) 33,5.

c) 36,0.

d) 34,7.

e) 30,7.

Letra C

Considerando o aumento linear, e senho y a incidência dessa doença, para cada 100.000 homens, temos:

$\frac{y-18}{42}=\frac{12,3}{29}=\boxed{y≅36,0}$

(Enem) Um administrador de um campo de futebol deseja recobri-lo com um tipo de grama que, em condições normais, cresce de acordo com o gráfico a seguir.

 

Ele precisa ter o campo pronto no dia 11 de junho de 2012, e o comprimento mínimo da grama nesse dia deve ser igual a 7 cm.

Supondo-se que o crescimento da grama se dê em condições normais, a grama deve ser plantada, no máximo, até o dia

A)17 de maio de 2012.

B)21 demaio de 2012.

C)23 de maio de 2012.

D)8 de junho de 2012.

E)9 de junho de 2012.

Letra B a resposta

A(2, 5) —> B(5, 11)

 

Equação da reta AB —> o coeficiente angular "a"; 

$a=\frac{\Delta y}{\Delta x}=\frac{11-5}{5-2}=\frac{6}{3}=2$ 

com f(x)= ax+b

e tomando o ponto A(2,5), calcularemos o coeficiente linear "b";

f(2)=2.2+b

 5=4+b

b=5-4

b=1

Assim nossa função é  y = 2.x + 1

 

Para y = 7

7 = 2.x + 1

2x=7-1

$2x=6$

$x=\frac{6}{2}$   

 x = 3 semanas

 

21 maio + 7 = 28 maio + 7 = 11 junho

(Enem) Certo município brasileiro cobra a conta de água de seus habitantes de acordo com o gráfico. O valor a ser pago depende do consumo mensal em m³.

 

Se um morador pagar uma conta de R$ 19,00, isso significa que ele consumiu

a)16 m³ de água.

b)17 m³ de água.

c)18 m³ de água.

d)19 m³ de água.

e)20 m³ de água.

(ACAFE Medicina 2014/1) Uma torneira gotejando diariamente é responsável por grandes desperdícios de água. Observe o gráfico que indica o desperdício de uma torneira. Se y representa o desperdício de água, em litros, e x representa o tempo, em dias, a relação entre x e y é:

Se y representa o desperdício de água, em litros, e x representa o tempo, em dias, a relação entre x e y é

 a)y = 2x

 b)y = $\frac{1}{2}x$

 c)y = 60x

 d)y = 60x + 1

 e)y = 80x + 50